就线性分类模型而言,可以将其表示为: $$ h_\theta(x)=g(\theta^Tx), \\ g(z) = 1\lbrace z \geq 0 \rbrace $$ 其中,训练集表示为: $$ S=\lbrace (x^{(i)}, y^{(i)}) \rbrace _ {i = 1} ^ m, (x^{(i)}, y^{(i)}) \sim {\cal D} $$ 这里假设了训练数据都是独立同分布的。
那么,我们认为,这个线性分类器的训练误差就可以表示为它分类错误的样本比例: $$ {\hat{\varepsilon}}(h_\theta) = {\hat{\varepsilon}}s(h\theta) = \frac{1}{m}\sum_{i=1}^m1\lbrace h_\theta (x^{(i)}) \neq y^{(i)} \rbrace $$ 在这里,我们把训练误差也称为风险(risk),由此我们导出了经验风险最小化。
经验风险最小化
Empirical Risk Minimization,ERM
经验风险最小化,最终导出一组参数,能够使得训练误差最小: $$ {\hat{\theta}} = \arg \min {\hat{\varepsilon}}s(h\theta) $$
我们再定义一个假设类${\cal{H}} = \lbrace h_\theta, \theta \in {\Bbb R}^{n+1} \rbrace$,它是所有假设的集合。在线性分类中,也就是所有线性分类器的集合。
那么,我们可以重新定义一次ERM: $$ {\hat h} = \mathop{\arg \min}_{h \in {\cal H}} {\hat \varepsilon}(h) $$ 对上述公式的直观理解就是:从假设类中选取一个假设,使得训练误差最小。我们这里用了$\hat{h}$表示估计,因为毕竟不可能得到最好的假设,只能得到对这个最好的假设的估计。
但这仍然不是目标,我们的目标是使得泛化误差 Generalization Error最小化,也即新的数据集上分类错误的概率: $$ \varepsilon(h)=P_{(x,y) \sim {\cal D}}(h(x) \neq y) $$ 接下去,为了证明:
-
(1)${\hat \varepsilon} \approx \varepsilon$,训练误差近似于泛化误差(理解为,泛化误差和训练误差之间的差异存在上界)
-
(2)ERM输出的泛化误差$\varepsilon({\hat h})$存在上界;
我们引出两个引理:
-
联合界引理(Union Bound)
$A_1, A_2, \ldots , A_k$是k个事件,他们之间并不一定是独立分布的,有: $$ P(A_1 \cup \ldots \cup A_k) \leq P(A_1) + \dots + P(A_k) $$
-
Hoeffding不等式(Hoeffding Inequality)
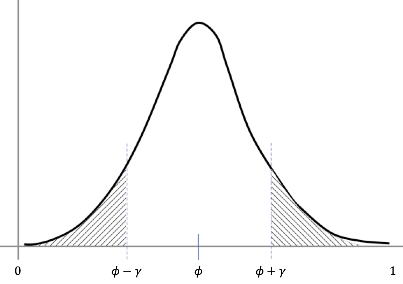
$z_1, \ldots z_m$是m个iid(independent and identically distribution,独立同分布),他们都服从伯努利分布,$P(z_i=1) = \phi$,那么对$\phi$的估计: $$ {\hat \phi} = \frac{1}{m}\sum_{i=1}^m z_i $$ 于是,给定$\gamma > 0$,有: $$ P(|{\hat{\phi}} - \phi| > \gamma) \leq 2 exp(-2\gamma^2m) $$
Hoeffding不等式的直观解释就是,下图中的阴影面积,会有上界。
一致收敛
Uniform Conversions
对于某个$h_j \in \cal{H}$,我们定义$z_i = 1 \lbrace h_j(x^{(i)}) \neq y^{(i)}\rbrace \in \lbrace{}$为第i个样本被分类错误的指示函数的值,对于logistic而言,它服从伯努利分布。
那么:
- 泛化误差:$P(z_i=1) = \varepsilon(h_j)$
- 训练误差:${\hat{\varepsilon}}(h_j) = \frac{1}{m}\sum_{i=1}^m z_i$
根据Hoeffding不等式,我们能够得到: $$ P(|{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| > \gamma) \leq 2e^{-2\gamma^2m} $$ 接着,我们定义训练误差和泛化误差之间的差大于$\gamma$($|{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| > \gamma$)为事件$A_j$,根据以上结论,我们可知: $$ P(A_j) \leq 2e^{-2\gamma^2m} $$ 那么根据联合界引理: $$ \begin{array}{l} & P(\exists h_j \in H, |{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| > \gamma) \\ = & P(A_1 \cup A_2 \cup \ldots \cup A_k) \\ \leq & \sum_{i=1}^k P(A_i) \\ \leq & \sum_{i=1}^k 2e^{-2\gamma^2m} \\ = & 2ke^{-2\gamma^2m} \end{array} $$ 可以表述为:存在$h_j$使$|{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| > \gamma$的概率$\leq 2ke^{-2\gamma^2m}$。
等价于:不存在$h_j$使$|{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| > \gamma$的概率$\geq 1 - 2ke^{-2\gamma^2m}$。
等价于:$\cal H$中任意的$h_j$使得$|{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| \leq \gamma$的概率$\geq 1 - 2ke^{-2\gamma^2m}$。
我们将上面这个结论称之为一致收敛 Uniform Conversions,也就是说事实上,所有的假设,训练误差和泛化误差之间都存在上界。
样本复杂度,误差界以及偏差方差权衡
上面的结论,我们可以引出以下的一些推论:
样本复杂度 Sample Complexity
给定$\gamma, \delta$,需要多大的训练集合($m$)?其中$\delta$指的是泛化误差和训练误差之差大于$\gamma$的概率。
我们知道,$\delta \leq 2ke^{-2\gamma^2m}$,可求解: $$ m \geq \frac{1}{2 \gamma ^ 2} log(\frac{2k}{\delta}) $$ 这个,也被称为样本复杂度(类似于时间复杂度),指的是,只要满足上面这个条件,任意$h \in \cal H$,都能得到$|{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| \leq \gamma$
误差界 Error Bound
给定$\delta, m$时,我们会得到多大的误差上界$\gamma$。
经过求解可以得到: $$ P(\forall h \in {\cal H}, |{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| \leq \sqrt{\frac{1}{2m}log(\frac{2k}{\delta})}) \geq 1 - \delta $$ 也就是误差上界是:$\gamma = \sqrt{\frac{1}{2m}log(\frac{2k}{\delta})}$。
偏差方差权衡 Bias Variance Tradeoff
我们定义: $$ \begin{align} {\hat h} &= \mathop{\arg \min}{h \in \cal H} {\hat \varepsilon}(h) \text{, 使得训练误差最小的h} &\tag{1} \\ h^\ast &= \mathop{\arg \min}{h \in \cal H} \varepsilon(h) \text{, 使得泛化误差最小的h} \tag{2} \end{align} $$ 假如: $$ \forall h \in {\cal H}, |{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| \leq \gamma \tag{3} $$
那么: $$ \begin{align} \varepsilon(\hat h) &\leq {\hat \varepsilon}({\hat h}) + \gamma, &\text{derived from (3)}\\ &\leq {\hat \varepsilon}(h^\ast) + \gamma, &\text{derived from (1)}\\ &\leq {\varepsilon(h^\ast)} + \gamma + \gamma, &\text{ derived from (3)} \end{align} $$ 于是,我们得到如下定理:
给定大小为$k$的假设集合$\cal H$,给定$m, \delta$,那么: $$ \varepsilon(\hat h) \leq \underbrace{(\min_{h \in {\cal H}}\varepsilon(h))}{\varepsilon(h^\ast)} + 2 \underbrace{\sqrt{\frac{1}{2m}log(\frac{2k}{\delta})}}{\gamma} $$ 的概率不低于$1-\delta$。
可以想象,为了得到最佳的假设$h^\ast$,我们尽可能增大$\cal H$(能够减小$\varepsilon(h^\ast)$),但随之而来的就是$\gamma$的增大,所以需要在这两者之间进行权衡,我们指的就是偏差方差权衡 Bias Variance Tradeoff。
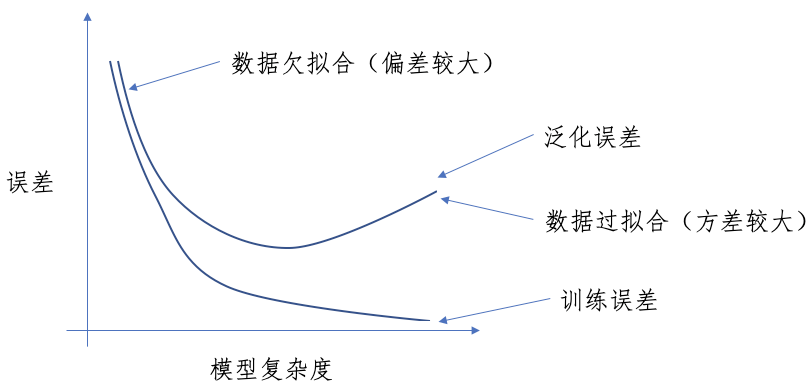
由此,我们得到一个推论:
给定$\delta, \gamma$,为了能够保证$\varepsilon(\hat h) \leq (\min_{h \in {\cal H}}\varepsilon(h)) + 2\gamma$的概率不小于$1-\delta$(ERM得到的假设的一般误差,与最佳假设的一般误差之间,差值不大于$2\gamma$)
我们需要保证: $$ m \geq \frac{1}{2\gamma^2}log(\frac{2k}{\delta}) $$